分类标签归档：聚类
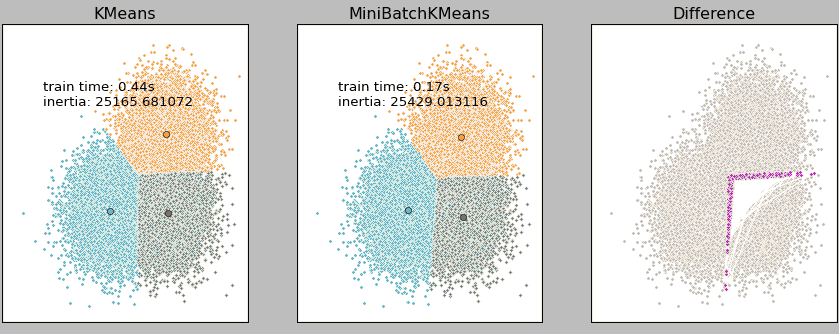
[K-Means算法]是常用的聚类算法，但其算法本身存在一定的问题，例如在大数据量下的计算时间过长就是一个重要问题。为此，Mini BatchK-Means，这个基于K-Means的变种聚类算法应运而生。 大数据量是什么量级？通过当样本量大于1万做聚类时，就需要考虑选用Mini Batch K-Means算法。但是，在选择算法时，除了算法效率（运行时间）外，算法运行的准确度也是选择算法的重要因素。Mini Batch
K-Means算法的准确度如何？
上图是我们队3万的样本点分别使用K-Means和Mini Batch KMeans进行聚类的结果，由结果可知，在3万样本点的基础上，二者
DBSCAN的全部英文是Density-Based Spatial Clustering of Applications with Noise，中文是“基于密度的带有噪声的空间聚类”。DBSCAN是一个比较有代表性的基于密度的聚类算法，与划分和层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声的空间数据库中发现任意形状的聚类。
该算法利用基于密度的聚类的概念，即要求聚类空间中的一定区域内（用Eps定义出的半径）所包含对象（点或其他空间对象）的数目不小于某一给定阈值（用MinPts定义的聚类点数）。
DBSCAN算法的显著优点是聚类能够 有效处理
在之前的文章里，介绍了比较传统的[K-Means聚类]、[Affinity Propagation(AP)聚类]、比K-Means更快的[Mini Batch K-Means]聚类以及[混合高斯模型Gaussian Mixture Model(GMM)]等聚类算法，今天介绍一个比较近代的一类算法——Spectral Clustering 中文通常称为“谱聚类”。
Spectral Clustering（谱聚类，有时也简称SC），其实是一类算法的统称。
它是一种基于图论的聚类方法（这点上跟AP类似，而K-Means是基于点与点的距离计算），它能够识别任意形状的样本空间且收敛于全局最有解，其基本思
Mean Shift算法，一般是指一个迭代的步骤，即先算出当前点的偏移均值，然后以此为新的起始点，继续移动，直到满足一定的结束条件。 Mean Shift算法是一种无参密度估计算法或称[核密度估计算法]，Mean shift是一个向量，它的方向指向当前点上概率密度梯度的方向。
所谓的核密度评估算法，指的是根据数据概率密度不断移动其均值质心（也就是算法的名称Mean Shift的含义）直到满足一定条件。
上图诠释了Mean Shift算法的基本工作原理，那么如何找到数据概率密度最大的区域？
数据最密集的地方，对应于概率密度最大的地方。我们可以对概率密度求梯度，梯度的方向就是概率密度增加最大的
Affinity Propagation聚类算法简称AP，是一个在07年发表在Science上面比较新的算法。
AP算法的基本思想是将全部样本看作网络的节点，然后通过网络中各条边的消息传递计算出各样本的聚类中心。聚类过程中，共有两种消息在各节点间传递，分别是吸引度(responsibility)和归属度(availability)。AP算法通过迭代过程不断更新每一个点的吸引度和归属度值，直到产生m个高质量的Exemplar（类似于质心），同时将其余的数据点分配到相应的聚类中。
在AP算法中有一些特殊名词：
聚类是数据挖掘中的基本任务，聚类是将大量数据集中具有“相似”特征的数据点划分为统一类别，并最终生成多个类的方法。
聚类分析的基本思想是“物以类聚、人以群分”，因此大量的数据集中必然存在相似的数据点，基于这个假设就可以将数据区分出来，并发现每个数据集（分类）的特征。
与聚类的概念类似的另外一个概念是“分类”，实际上二者经常被混用。但二者根本上是不同的：