Mean Shift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,然后以此为新的起始点,继续移动,直到满足一定的结束条件。 Mean Shift算法是一种无参密度估计算法或称[核密度估计算法],Mean shift是一个向量,它的方向指向当前点上概率密度梯度的方向。
所谓的核密度评估算法,指的是根据数据概率密度不断移动其均值质心(也就是算法的名称Mean Shift的含义)直到满足一定条件。
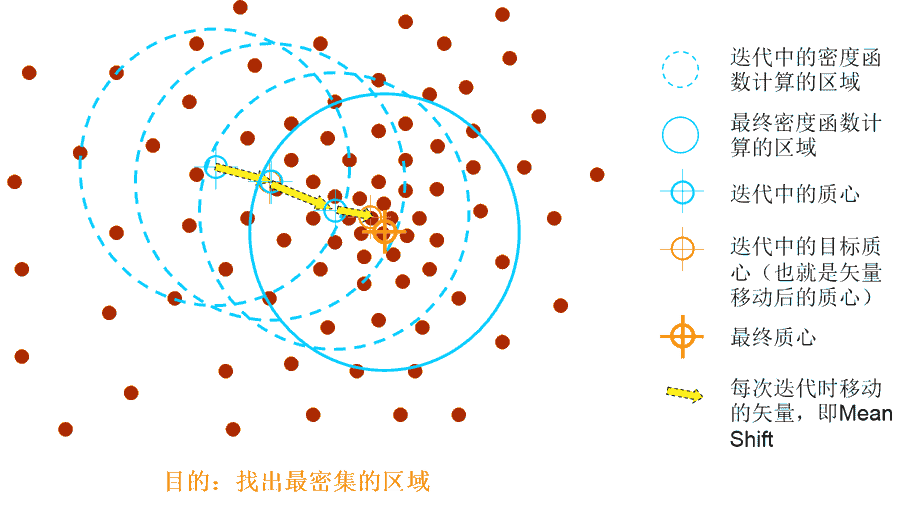
上图诠释了Mean Shift算法的基本工作原理,那么如何找到数据概率密度最大的区域?
数据最密集的地方,对应于概率密度最大的地方。我们可以对概率密度求梯度,梯度的方向就是概率密度增加最大的方向,从而也就是数据最密集的方向。 Mean Shift算法最常用于目标跟踪,它通过计算候选目标与目标模板之间相似度的概率密度分布,然后利用概率密度梯度下降的方向来获取匹配搜索的最佳路径,加速运动目标的定位和降低搜索的时间,因此在目标实时跟踪领域有着很高的应用价值。其优点是:
- 由于采用了统计特征,因此对噪声有很强的鲁棒性;
- 由于是一个单参数算法,容易作为一个模块和别的算法集成;
- 采用核函数直方图建模,对边缘阻挡、目标的旋转、变形以及背景运动都不敏感;
- 算法构造了一个可以用Mean Shift算法进行寻优的相似度函数。由于Mean Shift本质上是最陡下降法,因此其寻优过程收敛速度快,使得该算法具有很好的实时性。
同时,MeanShift算法也存在着一些缺点:
- 缺乏必要的模板更新;
- 跟踪过程中由于窗口宽度大小保持不变,当目标尺度有所变化时,跟踪就会失败;
- 当目标速度较快时,跟踪效果不好;
- 直方图特征在目标颜色特征描述方面略显匮乏,缺少空间信息.
Mean Shift的应用 Mean Shift算法在很多领域都有成功应用,例如图像平滑、图像分割、物体跟踪等,这些属于人工智能里面模式识别或计算机视觉的部分;另外也包括常规的聚类应用。
- 图像平滑:图像最大质量下的像素压缩;
- 图像分割:跟图像平滑类似的应用,但最终是将可以平滑的图像进行分离已达到前后景或固定物理分割的目的;
- 目标跟踪:例如针对监控视频中某个人物的动态跟踪;
- 常规聚类,如用户聚类等。
下面基于Python的机器学习库SKlearn中的MeanShift演示Mean Shift算法应用。 `
import numpy as np
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets.samples_generator import make_blobs
# 生成样本点
centers = [[1, 1], [-1, -1], [1, -1]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)
# 通过下列代码可自动检测bandwidth值
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)
ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
labels_unique = np.unique(labels)
n_clusters_ = len(labels_unique)
new_X = np.column_stack((X, labels))
print("number of estimated clusters : %d" % n_clusters_)
print("Top 10 samples:",new_X[:10])
# 图像输出
import matplotlib.pyplot as plt
from itertools import cycle
plt.figure(1)
plt.clf()
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
my_members = labels == k
cluster_center = cluster_centers[k]
plt.plot(X[my_members, 0], X[my_members, 1], col + '.')
plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col, markeredgecolor='k', markersize=14)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
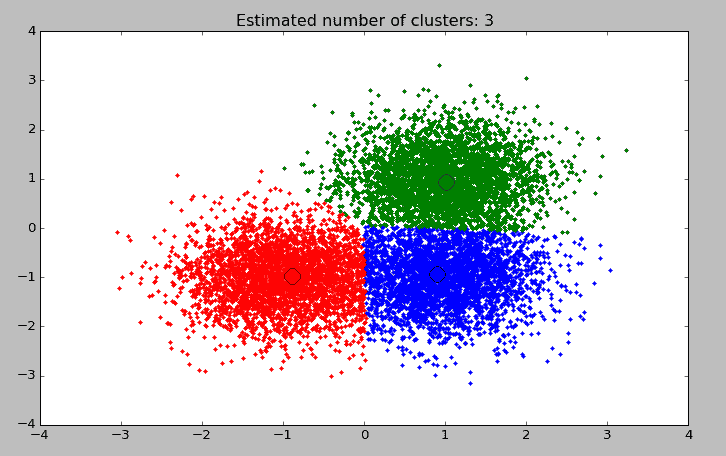
以下是代码执行结果
number of estimated clusters : 3
('Top 10 samples:', array(
[[ 1.8141499 , -1.45580736, 0. ],
[-0.66658907, -0.29515074, 2. ],
[-1.49755338, -0.96610942, 2. ],
[ 0.34816411, -0.69885676, 0. ],
[ 1.80841958, 2.14678071, 1. ],
[ 1.02185502, -0.9430071 , 0. ],
[ 1.58717372, -0.85057434, 0. ],
[ 2.25539903, -0.22049871, 0. ],
[ 0.30516472, -1.6391161 , 0. ],
[ 0.49500464, -0.76833638, 0. ]]))
MeanShift可配置的参数,其中重点是bandwidth值的设置。 `
class sklearn.cluster.MeanShift(bandwidth=None, seeds=None, bin_seeding=False, min_bin_freq=1, cluster_all=True)
尾巴
在上述实现算法中,我们强调了MeanShift具有很好的实时计算性,但由于Python中的该算法中默认情况下会使用sklearn.cluster.estimate_bandwidth函数进行自动计算bandwidth值,而klearn.cluster.estimate_bandwidth的可扩展性将会成为MeanShift在大量数据集下应用实时性的瓶颈。当然,解决方法是不使用其默认的bandwidth计算函数,而自己指定一个数值,这就要求操作人员对原始数据集、算法和应用场景有比较好的先验经验,一定程度上提高的应用要求。