在之前的文章里,介绍了比较传统的[K-Means聚类]、[Affinity Propagation(AP)聚类]、比K-Means更快的[Mini Batch K-Means]聚类以及[混合高斯模型Gaussian Mixture Model(GMM)]等聚类算法,今天介绍一个比较近代的一类算法——Spectral Clustering 中文通常称为“谱聚类”。
Spectral Clustering(谱聚类,有时也简称SC),其实是一类算法的统称。
它是一种基于图论的聚类方法(这点上跟AP类似,而K-Means是基于点与点的距离计算),它能够识别任意形状的样本空间且收敛于全局最有解,其基本思想是利用样本数据的 相似矩阵进行特征分解后得到的特征向量进行聚类。
为什么上文称谱聚类是“一类”算法?广义上来说,任何在演算法中用到SVD/特征值分解的,都叫Spectral Algorithm。 从传统的PCA/LDA,到比较近的Spectral Embedding/Clustering,都属于这类。
谱聚类和传统的聚类方法(如 K-means)相比有不少优点:
- Spectral Clustering 只需要数据之间的相似度矩阵就可以了,而不必像 K-Means 那样要求数据必须是 N 维欧氏空间中的向量。
- 由于抓住了主要矛盾,忽略了次要的东西,因此比传统的聚类算法更加健壮一些,对于不规则的误差数据不是那么敏感,而且结果也要好一些。事实上,在各种现代聚类算法的比较中,K-means 通常都是作为一个基准而存在的。
- 计算复杂度比 K-means 要小,特别是在像文本数据或者平凡的图像数据这样维度非常高的数据上运行的时候,理论上应该比K-Means更快速。(是这样吗?下文实验中有解答!)
K-Means一直以来都是距离算法中的经典算法,尤其通过minibatch“改良”后的K-Means在大数据应用中的效率瓶颈也得到极大改善。谱聚类这个相对的“晚生”是否真的如上述优点,接下来看实验数据。
实验一 关于准确度的较量
在此引用 Document clustering using locality preserving indexing中关于K-means 和 Spectral Clustering 应用到TDT2 和 Reuters-21578这两组数据的准确率对比结果:
从准确率结果可以看出,在不同的类别数量下,谱聚类的准确率都要高于K-Means。
实验二 关于运行时间的较量
在此使用Python机器学习库SKlearn中的spectral_clustering进行模拟实验,实验数据为随机生成的维度和样本量相同的矩阵,分别为10维、20维、30维。40维、50维、60维,对应到图中就是从0到5。其实我试着用更大的数据量去实验,但增加到70维的时候,spectral_clustering已经由于内存错误而崩掉了,所以足以看来他对于大数据量的应用还是不适合的。
另外,对于上文提到的spectral_clustering的计算复杂度要低于K-Means,因此理论上的运算时间要快,但实验结果却不能证明这个问题。
谱聚类应用
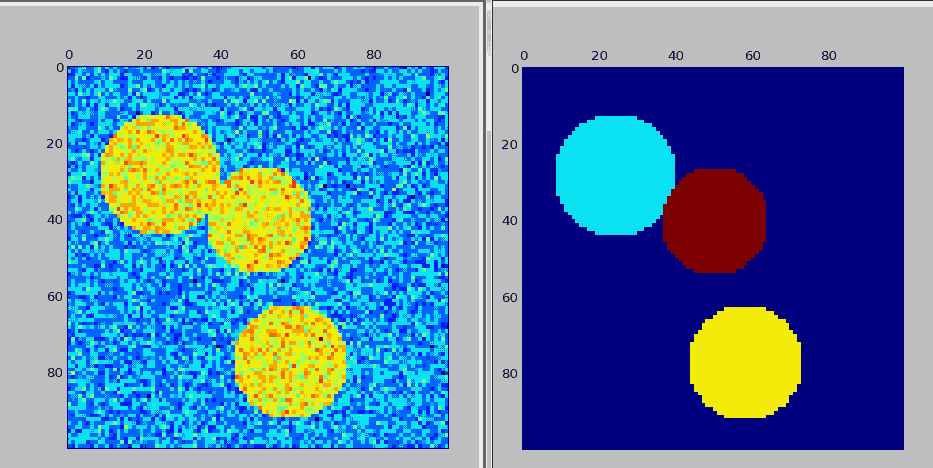
以下使用Python机器学习库SKlearn中的spectral_clustering进行聚类,目标是从一个图片中区分出人为构造出的图像边缘。 `
import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_extraction import image
from sklearn.cluster import spectral_clustering
# 生成原始图片信息
x, y = np.indices((l, l))
center1 = (28, 24)
center2 = (40, 50)
center3 = (77, 58)
radius1, radius2, radius3 = 16, 14, 15
circle1 = (x - center1[0]) ** 2 + (y - center1[1]) ** 2 < radius1 ** 2
circle2 = (x - center2[0]) ** 2 + (y - center2[1]) ** 2 < radius2 ** 2
circle3 = (x - center3[0]) ** 2 + (y - center3[1]) ** 2 < radius3 ** 2
# 生成包括3个圆的图片
img = circle1 + circle2 + circle3
mask = img.astype(bool)
img = img.astype(float)
img += 1 + 0.2 * np.random.randn(*img.shape)
graph = image.img_to_graph(img, mask=mask)
graph.data = np.exp(-graph.data / graph.data.std())
# 聚类输出
labels = spectral_clustering(graph, n_clusters=3)
label_im = -np.ones(mask.shape)
label_im[mask] = labels
plt.matshow(img)
plt.matshow(label_im)
plt.show()
以下是运行结果: 左边的图形是人为生成的原始图片,右边是识别图形边缘后的处理图片。
spectral_clustering可配置的参数如下,其中最主要的参数是affinity(数据集),n_clusters(聚类数)和assign_labels(聚类方法可选kmeans[默认], discretize): `
sklearn.cluster.spectral_clustering(affinity, n_clusters=8, n_components=None, eigen_solver=None, random_state=None, n_init=10, eigen_tol=0.0, assign_labels='kmeans')
谱聚类的应用场景:
- 图像切割;
- 数据聚类
尾巴 谱聚类适用的数据集有几个特点:
- 不适合聚类类别数特别多的数据;
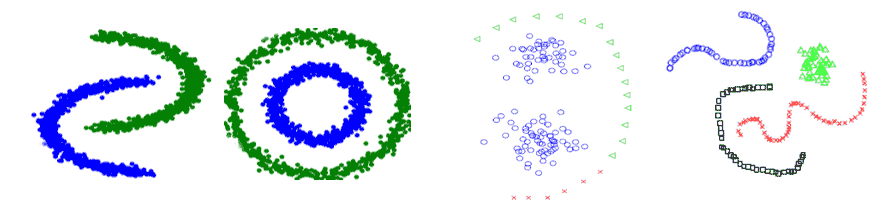
- 对于特殊数据集具有比较好的适应性,例如环形数据、非凸数据、交叉数据等非正常或规则下的数据,如下图: