分类目录归档：机器学习&数据挖掘
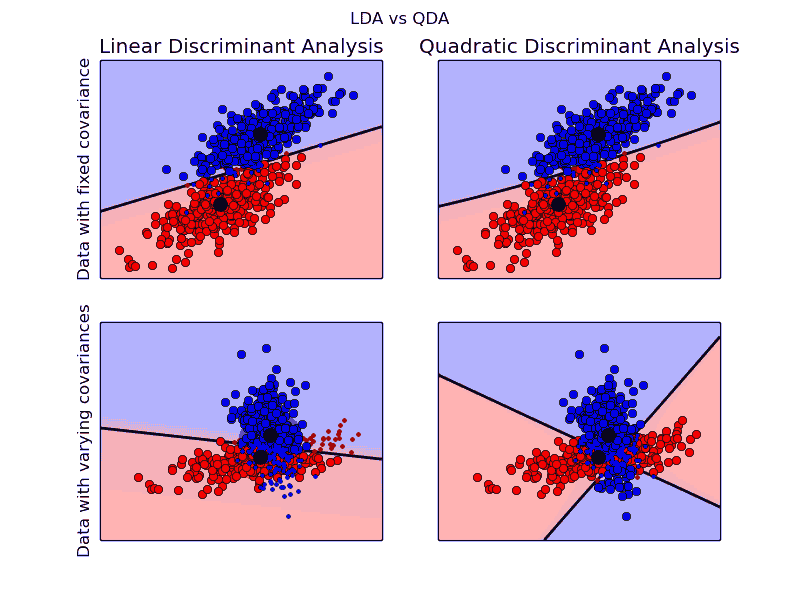
传统的降维方法，包括PCA、LDA等都是以观测数据点呈高斯分布模型为基本假设前提的，在已经先验经验知道观测数据集为非高斯分布模型的前提下，PCA和LDA的降维效果并不好；而本文介绍的ICA将适用于非高斯分析数据集，它是CIA，是主成分分析（PCA）和因子分析（Factor Analysis）的一种有效扩展。 独立成分分析（Independent component analysis，简称ICA）是一种利用统计原理进行计算的方法，它是一个线性变换，这个变换把数据或信号分离成统计独立的非高斯的信号源的线性组合。
独立成分分析的最重要的假设就是信号源统计独立，并且这个假设在大多数盲信号分离（blin
神经网络模型是模拟人类神经网络工作原理进行自我学习和演化的一种数据工作方法。神经网络在系统辨识、模式识别、智能控制等领域应用广泛，尤其在智能控制中被视为解决自动控制中控制器适应能力这个难题的关键钥匙之一。
神经网络理论是巨量信息并行处理和大规模平行计算的基础，是高度非线性动力学系统，又是自适应组织系统，可用来描述认知、决策及控制的智能行为．它的中心问题是智能的认知和模拟，更重要的是它具有“认知”、“意识”和“感情”等高级大脑功能。它再一次拓展了计算概念的内涵，使神经计算、进化计算成为新的学科，神经网络的软件模拟得到了广泛的应用。
既然神经网络模型是模拟人类神经网络的工作原理，那么首先来了解下人
与线性判别分析类似，二次判别分析是另外一种线性判别分析算法，二者拥有类似的算法特征，区别仅在于：当不同分类样本的协方差矩阵相同时，使用线性判别分析；当不同分类样本的协方差矩阵不同时，则应该使用二次判别。
为了清楚的了解LDA和QDA的应用差异，下图显示了在固定协方差矩阵以及不同协方差矩阵下LDA和QDA的表现差异：
由图中可以看出，在固定协方差矩阵下，LDA和QDA是没有分类结果差异的（上面两张图）；但在不同的协方差矩阵下，LDA和QDA的分类边界明显存在差异，而且LDA已经不能准确的划分数据（下面两张图）。
那么，协方差矩阵是什么？
在统计学中，有几个描述样本分布的基本指标，例如均值、方差
在面对海量数据或大数据进行数据挖掘时，通常会面临“维度灾难”，原因是数据集的维度可以不断增加而无穷多，但计算机的处理能力和速度却不是无限的；
另外，数据集的大量维度之间可能存在共线性的关系，这会直接导致学习模型的健壮性不够，甚至很多时候会失效。因此，我们需要一种可以降低维度数量并降低维度间共线性影响的方法——这就是降维的意义所在。
主成分分析是一种降维方法。主成分分析Principal component analysis(PCA)也称主分量分析，旨在利用降维的思想，把多维指标转化为少数几个综合维度，然后利用这些综合维度进行数据挖掘和学习，以代替原来利用所有维度进行挖掘学习的方法。
主成分分析
在《[新奇检测NoveltyDetection]》我们已经介绍了关于异常检测的基本理论、方法和基于python算法one-class SVM实现其中新奇检测的基本逻辑。本篇介绍异常检测的另外一个主题——离群点检测。
离群点检测是异常值检测的一种，其思路与新奇检测一致；区别在于离群点检测的原始观测数据集中已经包含异常值，而新奇检测则不包括。
以下是利用Python中SKlearn机器学习库的EllipticEnvelope实现对离群点的检测。EllipticEnvelope是Sklearn协方差估计中对高斯分布数据集的离群值检验方法，且该方法在高维度下的表现效果欠佳。
import numpy 在介绍核密度评估Kernel Density Estimation(KDE)之前，先介绍下密度估计的问题。
由给定样本集合求解随机变量的分布密度函数问题是概率统计学的基本问题之一。解决这一问题的方法包括参数估计和非参数估计。
参数估计又可分为参数回归分析和参数判别分析。在参数回归分析中，人们假定数据分布符合某种特定的性态，如线性、可化线性或指数性态等，然后在目标函数族中寻找特定的解，即确定回归模型中的未知参数。在参数判别分析中，人们需要假定作为判别依据的、随机取值的数据样本在各个可能的类别中都服从特定的分布。经验和理论说明，参数模型的这种基本假定与实际的物理模型之间常常存在较大的差距，这些方法