在面对海量数据或大数据进行数据挖掘时,通常会面临“维度灾难”,原因是数据集的维度可以不断增加而无穷多,但计算机的处理能力和速度却不是无限的;
另外,数据集的大量维度之间可能存在共线性的关系,这会直接导致学习模型的健壮性不够,甚至很多时候会失效。因此,我们需要一种可以降低维度数量并降低维度间共线性影响的方法——这就是降维的意义所在。
主成分分析是一种降维方法。主成分分析Principal component analysis(PCA)也称主分量分析,旨在利用降维的思想,把多维指标转化为少数几个综合维度,然后利用这些综合维度进行数据挖掘和学习,以代替原来利用所有维度进行挖掘学习的方法。
主成分分析的基本方法是按照一定的数学变换方法,把给定的一组相关变量(维度)通过 线性变换转成另一组不相关的变量,这些新的变量按照方差依次递减的顺序排列。
在数学变换中保持变量的总方差不变,使第一变量具有最大的方差,称为第一主成分,第二变量的方差次大,并且和第一变量不相关,称为第二主成分。依次类推,I个变量就有I个主成分。
到底主成分分析的结果是怎样的状态?下面简单举一个例子。
假设原始数据集中有10个维度分别是tenure、cardmon、lncardmon、cardten、lncardten、wiremon、lnwiremon、wireten、lnwireten、hourstv,现在用主成分分析进行降维,降维后的每个“因子”是: `
方程式用于 主成分-1
0.006831 * tenure +
0.007453 * cardmon +
0.1861 * lncardmon +
0.0001897 * cardten +
0.1338 * lncardten +
0.007552 * wiremon +
0.3688 * lnwiremon +
0.0001155 * wireten +
0.132 * lnwireten +
0.00006106 * hourstv +
-4.767
方程式用于 主成分-2
-0.005607 * tenure +
0.03288 * cardmon +
0.759 * lncardmon +
0.0002219 * cardten +
0.05385 * lncardten +
-0.01013 * wiremon +
-0.4433 * lnwiremon +
-0.0001222 * wireten +
-0.1354 * lnwireten +
0.008099 * hourstv +
-0.272
方程式用于 主成分-3
-0.01809 * tenure +
0.0124 * cardmon +
0.2859 * lncardmon +
-0.0002123 * cardten +
-0.2252 * lncardten +
0.0287 * wiremon +
1.193 * lnwiremon +
0.00002565 * wireten +
-0.1644 * lnwireten +
0.03984 * hourstv +
-4.076
方程式用于 主成分-4
0.004858 * tenure +
-0.00553 * cardmon +
-0.1352 * lncardmon +
0.00005099 * cardten +
0.03662 * lncardten +
-0.006129 * wiremon +
-0.2493 * lnwiremon +
0.00001144 * wireten +
0.04165 * lnwireten +
0.198 * hourstv +
-2.994
方程式用于 主成分-5
-0.01763 * tenure +
-0.005433 * cardmon +
0.5251 * lncardmon +
-0.001116 * cardten +
0.7426 * lncardten +
-0.004448 * wiremon +
0.7988 * lnwiremon +
-0.0005994 * wireten +
0.6897 * lnwireten +
0.00946 * hourstv +
-11.09
这就是主成分分析后提取的5个能代表原始10个维度的新“维度”。通过上述结果我们可以发现主成分(也就是新的“维度”)是一个线性方程,而且是多元一次的方程;其含义是无法被人类直接理解的,这意味着人类无法将特征提取的方法直接应用到主成分分析之上(在类似于特征提取或分类器的算法中,可以直接了解原始参与计算的每个维度的权重的高低)。但这没有关系,因为机器学习或数据挖掘不需要知道每个因子的具体含义,只需要知道用哪些因子,如何计算便能得到最终结果。
PCA可以对主成分分析的结果按重要性排序并根据用户需求只选择能代表大多数(甚至全部,如果你愿意)指标意义的成分,从而达到降维从而简化模型或是进行数据压缩的效果;另外,它是完全无参数限制的,这意味着无需人为设定参数,且先验经验都不需要,实用性和推广性非常强。但是,这个优点从另一个角度讲却是个缺点,因为它忽略了对具有先验经验的人群和应用场景的优化和应用,导致某些场景下缺少一定“高效果”的人工干预而导致无法达到预期效果。
下面应用一个案例,用Python的机器学习库SKlearn中的PCA来对数据进行降维。原始数据集中有4个维度,现在要通过PCA转换成2个维度。实现过程如下:
from sklearn import datasets
from sklearn.decomposition import PCA
iris = datasets.load_iris()
X = iris.data
print ('first 10 raw samples:', X[:10])
pca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)
print ('first 10 transformed samples:', X_r[:10])
print ('variance:',pca.explained_variance_ratio_)
降维后的原始数据集中的4个维度被转化成两个维度,结果如下:
('first 10 raw samples:', array([[ 5.1, 3.5, 1.4, 0.2],
[ 4.9, 3. , 1.4, 0.2],
[ 4.7, 3.2, 1.3, 0.2],
[ 4.6, 3.1, 1.5, 0.2],
[ 5. , 3.6, 1.4, 0.2],
[ 5.4, 3.9, 1.7, 0.4],
[ 4.6, 3.4, 1.4, 0.3],
[ 5. , 3.4, 1.5, 0.2],
[ 4.4, 2.9, 1.4, 0.2],
[ 4.9, 3.1, 1.5, 0.1]]))
('first 10 transformed samples:', array([[-2.68420713, -0.32660731],
[-2.71539062, 0.16955685],
[-2.88981954, 0.13734561],
[-2.7464372 , 0.31112432],
[-2.72859298, -0.33392456],
[-2.27989736, -0.74778271],
[-2.82089068, 0.08210451],
[-2.62648199, -0.17040535],
[-2.88795857, 0.57079803],
[-2.67384469, 0.1066917 ]]))
('variance:', array([ 0.92461621, 0.05301557]))
PCA应用的关键是找到能代表原始数据最大特征的几个主成分,因此上述代码中通过pca.explained_variance_ratio_来查看每个主成分能表达原始数据的方差,实际应用时可写一个循环来判定不同主成分数量下的方差之和,同时配合一个阀值来选择PCA中components的个数。例如可设定能代表原始数据集95%的方差的主成分就可以,那么当循环出来的主成分的方差之和大于95%就可以停止循环。然后进行接下来的数据处理工作。
PCA可配置的参数如下:`
class sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)
应用场景:
- 如本文开始所说的,PCA的应用是降维,用在所有大量数据集建模处理之前的降维过程,因此它是数据预处理过程的一步。
尾巴
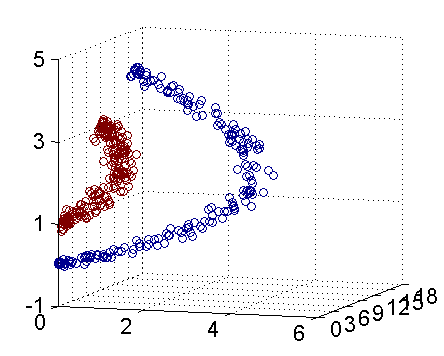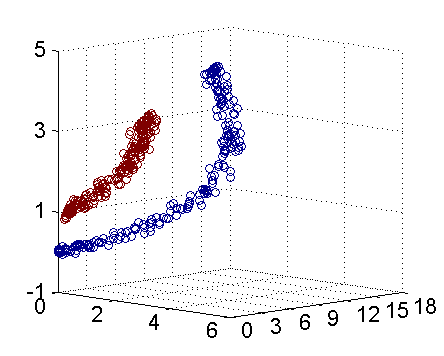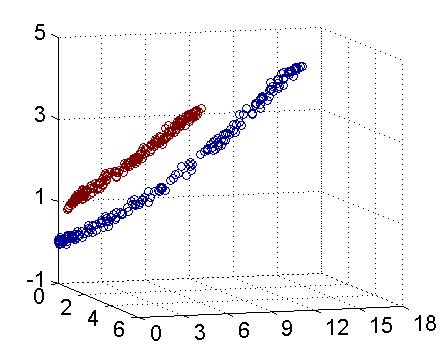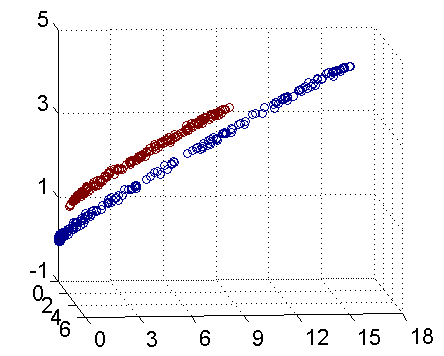
从主观的理解上,主成分分析到底是什么?它其实是对数据在高维空间下的一个投影转换,通过一定的投影规则将原来从一个角度看到的多个维度映射成较少的维度。到底什么是映射,下面的图就可以很好地解释这个问题——正常角度看是两个半椭圆形分布的数据集,但经过旋转(映射)之后是两条线性分布数据集。