混合高斯模型(Gaussian Mixture Model,简称GMM)是用高斯概率密度函数(正态分布曲线)精确地量化事物,将一个事物分解为若干的基于高斯概率密度函数(正态分布曲线)形成的模型。通俗点讲,无论观测数据集如何分布以及呈现何种规律,都可以通过多个单一高斯模型的混合进行拟合。
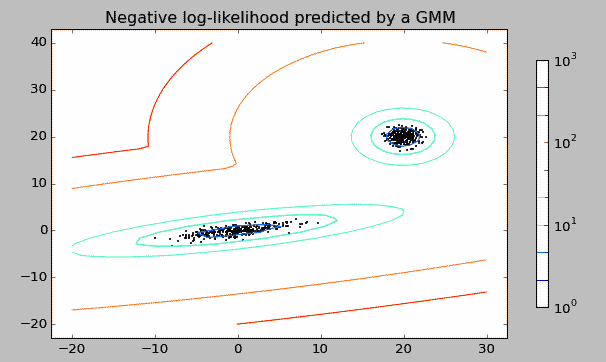
如下图是一个观测数据集,数据集明显分为两个聚集核心,我们通过两个单一的高斯模型混合成一个复杂模型来拟合数据。这就是一个混合高斯模型。
既然混合高斯模型是由n个(或多个)单高斯模型组成,那么首先了解下单高斯模型(Single Mixture Model,简称SMM)。
最常见的单高斯模型(或者叫单高斯分布)就是钟形曲线,只不过钟形曲线只是一维下的高斯分布。
高斯分布(Gaussian distribution)又叫正态分布(Normal distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。因其曲线呈钟形,因此人们又经常称之为钟形曲线。
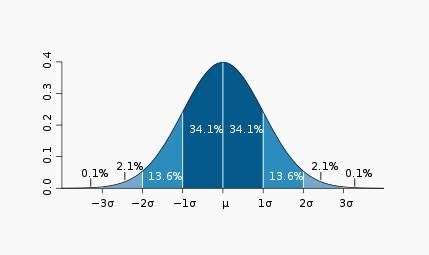
如下图为标准正态分布图:
它的基本定义是:若随机变量X服从一个数学期望为μ、方差为σ^2的高斯分布,则记为N(μ,σ^2)。数学期望μ指的是均值(算术平均值),σ为方标准差(方差开平方后得到标准差)。高斯分布的概率密度函数为:
上述公式只是一维下的高斯分布模型,多维高斯分布模型下概率密度函数如下:
上述公式中,x是维度为d的列向量,u是模型期望,Σ是模型方差。在实际应用中u通常用样本均值来代替,Σ通常用样本方差来代替。很容易判断一个样x本是否属于类别C。因为每个类别都有自己的u和Σ,把x代入公式中,当概率大于一定阈值时我们就认为x属于C类。
从几何形状上讲,单高斯分布模型在二维空间应该近似于椭圆(如本文最开始的图形),在三维空间上近似于椭球。但单高斯分布模型的问题是在很多分类问题中,属于同一类别的样本点并不满足“椭圆”分布的特性。因此,就需要引入高斯混合模型来解决这个问题。
我们可以用不同的分布来随意地构造 XX Mixture Model(例如泊松混合模型等),但由于GMM的计算性能强、拟合程度高等因素导致其最为流行。另外,混合模型本身也可以变得非常复杂,通过增加 Model的个数,改变权重的计算方法等,我们可以任意地逼近任何连续的概率密度分布。
那么,基于单高斯模型的混合高斯模型公式定义如下:
其中,K需要事先确定好,就像K-means中的K一样,只要K足够大,这个XX Mixture Model就会变得足够复杂,就可以用来逼近任意连续的概率密度分布。πk是权值因子。其中的任意一个高斯分布N(x;uk,Σk) 叫作这个模型的一个component(成分)。GMM是一种聚类算法,每个component就是一个聚类中心。
既然已经了解模型的定义,如何确定这些参数值?GMM通常使用最大期望( Expectation Maximum,简称EM)进行参数评估。EM算法的基本思路是:随机初始化一组参数θ(0),根据后验概率Pr(Y|X;θ)来更新Y的期望E(Y),然后用E(Y)代替Y求出新的模型参数θ(1)。如此迭代直到θ趋于稳定。
接下来使用Python的机器学习库SKlearn中的GMM算法演示实例——使用GMM来做分类。
import numpy as np
from sklearn import mixture
#生成随机观测点,含有2个聚集核心
obs = np.concatenate((np.random.randn(100, 1), 10 + np.random.randn(300, 1)))
clf = mixture.GMM(n_components=2)
print obs[:10]
clf.fit(obs)
#预测
print clf.predict([[0], [2], [9], [10]])
运行结果是:
('first 10 samples:',
array([[-1.67944936],
[ 0.64083316],
[ 0.21439992],
[-0.45738897],
[ 0.01882893],
[ 0.71916592],
[ 1.53913442],
[-0.07888893],
[ 0.19748583],
[-0.69922825]]))
[1, 1, 0, 0]
在该函数中,可配置的参数如下:
class sklearn.mixture.GMM(n_components=1, covariance_type='diag', random_state=None, thresh=None, tol=0.001, min_covar=0.001, n_iter=100, n_init=1, params='wmc', init_params='wmc')
混合高斯模型的应用场景包括:
- 数据集分类,如会员分类;
- 图像分割以及以及特征抽取,例如在视频中跟踪人物以及区分动作,识别汽车、建筑物等;
- 语音分割以及特征特征抽取,例如从一堆杂乱的声音中提取某个人的声音,从音乐中提取背景音乐,从大自然中提取地震的声音等。
尾巴
GMM与k-means聚类相似,也使用迭代算法计算并最终收敛到局部最优。但高斯混合模型在各类尺寸不同、聚类间有相关关系的的时候可能比k-means聚类更合适;GMM 是基于概率密度函数进行学习,所以除了在聚类应用外,还经常应用于密度检测(density estimation );另外,k-means 的结果是每个观测点一定被分类到某个数据集类别中,而 GMM 则给出的是被分类到不同数据集类别中的概率(又被称为软分类softassignment )。
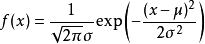
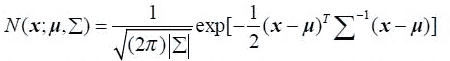

求问:对于GMM概念的解释(混合高斯模型(Gaussian Mixture Model,简称GMM)是用高斯概率密度函数(正态分布曲线)精确地量化事物,将一个事物分解为若干的基于高斯概率密度函数(正态分布曲线)形成的模型。通俗点讲,无论观测数据集如何分布以及呈现何种规律,都可以通过多个单一高斯模型的混合进行拟合。)这段话来自哪本书或者论文?我想引用一下。谢谢!
这段话记不太清了,貌似没有固定出处,是我个人的理解~~