Python的科学计算和数据挖掘相关库中,pandas和statsmodels都提供了时间序列相关分析功能,本示例使用的是statsmodels做时间序列预测应用。有关时间序列算法的选择,实际场景中最常用的是ARIMA或ARMA了,因此本示例将使用ARIMA/ARMA来做时间序列分析。
对于这两种时间序列方法而言,应用的难点是如何根据不同的场景判断参数值(即p、d、q)。本示例将设置判断阀值,通过自动化的程序方式来完成自动的ARIMA/ARMA的参数(p、d、q)选择以及模型训练,降低时间序列算法应用的难度。
示例中模拟的是针对具有时间序列特征的数据集做未来时间序列的预测,数据源文件time_series.txt可以从《Python数据分析与数据化运营》的“附件-chapter4”中找到。
第一部分导入库
statsmodels库里面的plot_acf、plot_pacf用于acf和pacf图形检验分析,adfuller、acorr_ljungbox用于adf检验和随机性检验,ARMA库做时间序列分析,matplotlib和prettytable做图形和表格格式化输出。
# 导入库
import pandas as pd # pandas库
import numpy as np # numpy库
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf # acf和pacf展示库
from statsmodels.tsa.stattools import adfuller # adf检验库
from statsmodels.stats.diagnostic import acorr_ljungbox # 随机性检验库
from statsmodels.tsa.arima_model import ARMA # ARMA库
import matplotlib.pyplot as plt # matplotlib图形展示库
import prettytable # 导入表格库
提示 ARIMA相对于ARMA多了一步差分的过程,但是由于statsmodels中的ARIMA对差分的支持不太好,最多只能多2阶差分,其实用性会大打折扣(其实2阶差分已经可以满足90%以上的场景了)。所以,在实际应用中,我们会手动做数据平稳性处理,然后将平稳数据传给ARMA模型做训练,完成ARIMA的时间序列分析。
第二部分定义一个名为pre_table的函数
该函数用来展示格式化表格数据,方便每次展示时调用而无需重复编写代码。
该函数的输入有2个参数:
- table_name:表格名称,字符串列表;
- table_rows:表格内容,嵌套列表,考虑到在添加内容时,可能会有批量添加的模式,因此批量添加的数据记录行需要转换为嵌套列表的形式,例如[[1,2,3,4],[2,2,3,4]]为要添加的两条数据记录;即使只有一条数据记录,也要写成嵌套列表的形式,例如[[1,2,3,4]]。
返回一个包含内容的可打印对象。
# 多次用到的表格
def pre_table(table_name, table_rows):
'''
:param table_name: 表格名称,字符串列表
:param table_rows: 表格内容,嵌套列表
:return: 展示表格对象
'''
table = prettytable.PrettyTable() # 创建表格实例
table.field_names = table_name # 定义表格列名
for i in table_rows: # 循环读多条数据
table.add_row(i) # 增加数据
return table
函数功能中,先通过prettytable.PrettyTable创建表格对象实例,然后通过实例的field_names方法增加表格名称,通过一个for循环将table_rows中的多个嵌套表格内容读出,并使用表格实例的add_row方法增加行数据。
第三部分定义一个名为get_best_log的函数
该函数用于数据平稳处理。该函数的输入参数有5个:
- ts:时间序列数据,Series类型
- max_log:最大log处理的次数,默认值为5,int型
- rule1:rule1规则布尔值,默认值为True,布尔型
- rule2:rule2规则布尔值,默认值为True,布尔型
返回:达到平稳处理的最佳log处理次数和处理后的时间序列
# 数据平稳处理
def get_best_log(ts, max_log=5, rule1=True, rule2=True):
'''
:param ts: 时间序列数据,Series类型
:param max_log: 最大log处理的次数,int型
:param rule1: rule1规则布尔值,布尔型
:param rule2: rule2规则布尔值,布尔型
:return: 达到平稳处理的最佳次数值和处理后的时间序列
'''
if rule1 and rule2: # 如果两个规则同时满足
return 0, ts # 直接返回0和原始时间序列数据
else: # 只要有一个规则不满足
for i in range(1, max_log): # 循环做log处理
ts = np.log(ts) # log处理
lbvalue, pvalue1 = acorr_ljungbox(ts, lags=1) # 白噪声检验结果
adf, pvalue2, usedlag, nobs, critical_values, icbest = adfuller(ts) # ADF检验
rule_1 = (adf < critical_values['1%'] and adf < critical_values['5%'] and adf < critical_values['10%'] and pvalue1 < 0.01) # 稳定性检验
rule_2 = (pvalue2 < 0.05) # 白噪声检验
rule_3 = (i < 5)
if rule_1 and rule_2 and rule_3: # 如果同时满足条件
print ('The best log n is: {0}'.format(i)) # 打印输出最佳次数
return i, ts # 返回最佳次数和处理后的时间序列
该函数功能中,先通过rule1 和rule2条件判断输入的两个规则是否同时满足,如果同时满足则说明该时间序列是平稳的,无需做任何平稳性处理;否则使用对数方法(numpy.log)做平稳性处理:
通过for循环按照指定的最大处理次数做循环处理,一般情况下做2次log处理就能满足90%的时间序列平稳性。
每次处理后使用acorr_ljungbox做白噪声检验、使用adfuller方法做ADF检验,如果二者检验的结果能够符合两个规则的阀值设定并且i的值在5以内,那么返回平稳处理的次数以及处理后的时间序列;否则终止程序。平稳处理的次数用于后期数据的还原,处理后的时间序列用于ARMA模型中的时间序列的输入数据集。
相关知识点:时间序列数据的平稳性
平稳性是做时间序列分析的前提条件,所谓平稳通俗理解就是数据没有随着时间呈现明显的趋势和规律,例如剧烈波动、递增、递减等,而是相对均匀且随机的分布在均值附近。在ARIMA模型中的I就是对数据做差分以实现数据的平稳,而ARIMA关键参数p、d、q中的d即时间序列成为平稳时所做的差分次数。
如何判断时间序列数据是否需要平稳性处理?
- 观察法:通过输出时间序列图发现数据是否平稳。本示例中的adf_val函数便有含有该方法。
- 自相关和偏相关法:通过观察自相关和偏相关的系数分析数据是否平稳。
- ADF检验:通过ADF检验得到的显著性水平分析数据是否平稳。本示例中的adf_val函数便有含有该方法。
实现数据的平稳有以下几种方法:
- 对数法:对数处理可以减小数据的波动,使其线性规律更加明显。但需要注意的是对数处理只能针对时间序列的值大于0的数据集。
- 差分法:一般来说,非纯随机的时间序列经一阶差分或者二阶差分之后就会变得平稳(statsmodels的ARIMA模型自动支持数据差分,但最大为2阶差分)。
- 平滑法:根据平滑技术的不同,可分为移动平均法和指数平均法,这两个都是最基本的时间序列方法。
- 分解法:将时序数据分离成不同的成分,包括成长期趋势、季节趋势和随机成分等。
第四部分定义了一个名为recover_log的函数
该函数目的是还原经过平稳处理的数据。在经过平稳性处理之后,原有的时间序列训练集已经被更改,通过ARMA得到的预测数据也是经过平稳处理后的数据,该数据要使用必须经过还原。该函数的参数:
- ts:经过log方法平稳处理的时间序列,Series类型
- log_n:log方法处理的次数,int型
返回:还原后的时间序列
# 还原经过平稳处理的数据
def recover_log(ts, log_n):
'''
:param ts: 经过log方法平稳处理的时间序列,Series类型
:param log_n: log方法处理的次数,int型
:return: 还原后的时间序列
'''
for i in range(1, log_n + 1): # 循环多次
ts = np.exp(ts) # log方法还原
return ts # 返回时间序列
该函数的功能中直接通过for循环通过平稳性处理得到的最佳处理次数,使用numpy的exp方法做逆对数处理得到原始时间序列值。
第五部分定义了一个名为adf_val的函数
该函数用于平稳性检验。该平稳性检验实现了时间序列图、acf图、pacf图、ADF检验数据等多种检验方法的数据和图形输出。函数的参数:
- ts:时间序列数据,Series类型
- ts_title:自定义的时间序列图的标题名称,字符串
- acf_title:自定义的acf图的标题名称,字符串
- pacf_title:自定义的pacf图的标题名称,字符串
返回:adf值、adf的p值、三种状态(1%、5%、10%)的检验值,这些值是用来构成rule1的判断规则的参数值。
# 平稳性检验
def adf_val(ts, ts_title, acf_title, pacf_title):
'''
:param ts: 时间序列数据,Series类型
:param ts_title: 时间序列图的标题名称,字符串
:param acf_title: acf图的标题名称,字符串
:param pacf_title: pacf图的标题名称,字符串
:return: adf值、adf的p值、三种状态的检验值
'''
plt.figure()
plt.plot(ts) # 时间序列图
plt.title(ts_title) # 时间序列标题
plt.show()
plot_acf(ts, lags=20, title=acf_title).show() # 自相关检测
plot_pacf(ts, lags=20, title=pacf_title).show() # 偏相关检测
adf, pvalue, usedlag, nobs, critical_values, icbest = adfuller(ts) # 平稳性检验
table_name = ['adf', 'pvalue', 'usedlag', 'nobs', 'critical_values', 'icbest'] # 表格列名列表
table_rows = [[adf, pvalue, usedlag, nobs, critical_values, icbest]] # 表格行数据,嵌套列表
adf_table = pre_table(table_name, table_rows) # 获得平稳性展示表格对象
print ('stochastic score') # 打印标题
print (adf_table) # 打印展示表格
return adf, pvalue, critical_values, # 返回adf值、adf的p值、三种状态的检验值
该函数的功能中,先调用Matplotlib的plot方法直接输出时间序列图,然后使用statsmodels.graphics.tsaplots的plot_acf和plot_pacf方法分别输出自相关和偏相关检测图,使用adfuller方法做平稳性检验;接着通过定义要输出的表格的列名列表和行记录列表,调用pre_table方法形成格式化表格并打印输出。
第六部分定义了一个名为acorr_val的函数
该函数用于白噪声(随机性)检验。函数参数:
- ts:时间序列数据,Series类型
返回:白噪声检验的P值,用来做rule2判断规则的参数值。函数参数:
# 白噪声(随机性)检验
def acorr_val(ts):
'''
:param ts: 时间序列数据,Series类型
:return: 白噪声检验的P值和展示数据表格对象
'''
lbvalue, pvalue = acorr_ljungbox(ts, lags=1) # 白噪声检验
table_name = ['lbvalue', 'pvalue'] # 表格列名列表
table_rows = [[lbvalue, pvalue]] # 表格行数据,嵌套列表
acorr_ljungbox_table = pre_table(table_name, table_rows)
print ('stationarity score') # 打印标题
print (acorr_ljungbox_table) # 打印展示表格
return pvalue # 返回白噪声检验的P值和展示数据表格对象
函数功能中,使用acorr_ljungbox返回白噪声检验结果,然后将调用pre_table将数据格式化为表格形式打印出来。
相关知识点:白噪声检验
白噪声(white noise)检验也称为随机性检验,用于检验时间序列的各项数值之间是否具有任何相关关系,白噪声分布是应用时间序列分析的前提。检测时间序列是否属于随机性分布,可通过图形和Ljung Box方法检验。
- 图形法:时间序列应该是围绕均值随机性上下分布的状态。
- Ljung Box法:是对时间序列是否存在滞后相关的一种统计检验,判断序列总体的相关性或者说随机性是否存在。
白噪声检验通常和数据平稳性检验是协同进行数据检验的,这意味着如果平稳性检验通过,白噪声检验一般也会通过。
第七部分定义了一个名为arma_fit的函数
该函数用于做arma最优模型训练。该模型实现的是基于给定的时间序列数据,自动寻找BIC最小时的p和q的阶数,并形成训练好的ARMA模型。函数参数:
- ts:时间序列数据,Series类型
返回:最优状态下arma模型对象,用于后续模型训练效果评估和预测应用。需要注意的是,输入的ts时间序列数据是已经经过平稳性处理,并满足平稳性和白噪音检验的时间序列数据。
# arma最优模型训练
def arma_fit(ts):
'''
:param ts: 时间序列数据,Series类型
:return: 最优状态下的p值、q值、arma模型对象、pdq数据框和展示参数表格对象
'''
max_count = int(len(ts) / 10) # 最大循环次数最大定义为记录数的10%
bic = float('inf') # 初始值为正无穷
tmp_score = [] # 临时p、q、aic、bic和hqic的值的列表
for tmp_p in range(max_count + 1): # p循环max_count+1次
for tmp_q in range(max_count + 1): # q循环max_count+1次
model = ARMA(ts, order=(tmp_p, tmp_q)) # 创建ARMA模型对象
try:
results_ARMA = model.fit(disp=-1, method='css') # ARMA模型训练
except:
continue # 遇到报错继续
finally:
tmp_aic = results_ARMA.aic # 模型的获得aic
tmp_bic = results_ARMA.bic # 模型的获得bic
tmp_hqic = results_ARMA.hqic # 模型的获得hqic
tmp_score.append([tmp_p, tmp_q, tmp_aic, tmp_bic, tmp_hqic]) # 追加每个模型的训练参数和结果
if tmp_bic < bic: # 如果模型bic小于最小值,那么获得最优模型ARMA的下列参数:
p = tmp_p # 最优模型ARMA的p值
q = tmp_q # 最优模型ARMA的q值
model_arma = results_ARMA # 最优模型ARMA的模型对象
aic = tmp_bic # 最优模型ARMA的aic
bic = tmp_bic # 最优模型ARMA的bic
hqic = tmp_bic # 最优模型ARMA的hqic
pdq_metrix = np.array(tmp_score) # 将嵌套列表转换为矩阵
pdq_pd = pd.DataFrame(pdq_metrix, columns=['p', 'q', 'aic', 'bic', 'hqic']) # 基于矩阵创建数据框
table_name = ['p', 'q', 'aic', 'bic', 'hqic'] # 表格列名列表
table_rows = [[p, q, aic, bic, hqic]] # 表格行数据,嵌套列表
parameter_table = pre_table(table_name, table_rows) # 获得最佳ARMA模型结果展示表格对象
print ('each p/q traning record') # 打印标题
print (pdq_pd) # 打印输出每次ARMA拟合结果,包含p、d、q以及对应的AIC、BIC、HQIC
print ('best p and q') # 打印标题
print (parameter_table) # 输出最佳ARMA模型结果展示表格对象
return model_arma # 最优状态下的arma模型对象
函数实现功能中,先定义了几个值。默认p和q阶数的最大值为记录数的10%;判断最佳ARMA模型的方法是BIC方法,即选择最小的BIC值时的q和p的值,因此通过float('inf')来定义一个BIC值为正无穷,后续模型得到BIC值更小时选择对应的参数信息;tmp_score为临时p、q、aic、bic和hqic的值的列表,该列表将嵌套每次训练形成的评估参数结果集。
接下来的循环主体,将通过p和q的嵌套循环实现。
- 最内层循环中,先通过ARMA方法基于输入的时间序列和循环得到的p、q值创建模型对象。
- 然后应用模型对象的fit方法做模型训练,fit中的参数disp用来控制不打印收敛信息,mothed控制最大似然的计算方法是条件平方和似然度最大化。
- 在应用fit过程中,由于多次循环可能会报错导致循环中止,因此使用了try、except和finally进行控制,这三个语句的含义为执行try中的程序,如果遇到错误则执行except中的程序,最终无论是否报错都要执行finally中的程序。在finally语句中,通过fit后返回的结果类的aic、bic和hqic三个参数值,然后将p、q、aic、bic、hqic以列表的形式追加到临时列表中;如果判断bic的值比最小值要小,那么认为该值下的模型为更优模型,将其p、q、aic、bic和hqic的值存储下来。
- 最后将临时列表tmp_score转换为矩阵,并基于该矩阵创建用于展示每次循环数据的详细数据;然后基于最优模型的数据创建格式化展示列表并分别输出详细数据和最优模型对象。
注意
statsmodels中的ARMA通过应用fit方法后,返回的对象是一个ARMAResults类,而不再是原有的model(ARMA模型对象)本身,这一点跟sklearn不同,因此无法直接通过model本身获取模型的参数和评估指标等信息,而要通过ARMAResults来获取。
相关知识点:statsmodels中的ARMA
statsmodels常用的时间序列模型包括AR、ARMA和ARIMA都集中在statsmodels.tsa.arima_model下面。ARMA(p,q)是AR(p)和MA(q)模型的组合,关于p和q的选择,一种方法是观察自相关图ACF和偏相关图PACF,通过截尾、拖尾等信息分析应用的模型以及适应的p和q的阶数;另一种方法是通过循环的方法,遍历所有条件并通过AIC、BIC值自动确定阶数。
ARMA(以及statsmodels中的其他算法)跟sklearn中的算法类似,也都有方法和属性两种应用方式。常用的ARMA方法:
- fit:使用卡尔曼滤波器的最大似然法拟合ARMA模型。
- from_formula:基于给定的公式和数据框创建模型。
- geterrors:基于给定的参数获取ARMA进程的错误。
- hessian:基于给定的参数计算Hessian信息。
- loglike:计算ARMA模型的对数似然。
- loglike_css:条件求和方差似然函数。
- predict:应用ARMA模型做预测。
- score:得分函数。
第八部分定义了一个名为train_test的函数
该函数用于时间序列的模型训练和效果评估。该函数可将训练的时间序列内预测值与实际值做比较,并输出RMSE(均方根误差)和时间序列对比图。函数参数:
- model_arma:最优ARMA模型对象
- ts:时间序列数据,Series类型
- log_n:平稳性处理的log的次数,int型
- rule1:rule1规则布尔值,布尔型
- rule2:rule2规则布尔值,布尔型
返回:还原后的时间序列,该时间序列用于在时间序列外做预测后的图形展示。
# 模型训练和效果评估
def train_test(model_arma, ts, log_n, rule1=True, rule2=True):
'''
:param model_arma: 最优ARMA模型对象
:param ts: 时间序列数据,Series类型
:param log_n: 平稳性处理的log的次数,int型
:param rule1: rule1规则布尔值,布尔型
:param rule2: rule2规则布尔值,布尔型
:return: 还原后的时间序列
'''
train_predict = model_arma.predict() # 得到训练集的预测时间序列
if not (rule1 and rule2): # 如果两个条件有任意一个不满足
train_predict = recover_log(train_predict, log_n) # 恢复平稳性处理前的真实时间序列值
ts = recover_log(ts, log_n) # 时间序列还原处理
ts_data_new = ts[train_predict.index] # 将原始时间序列数据的长度与预测的周期对齐
RMSE = np.sqrt(np.sum((train_predict - ts_data_new) ** 2) / ts_data_new.size) # 求RMSE
# 对比训练集的预测和真实数据
plt.figure() # 创建画布
train_predict.plot(label='predicted data', style='--') # 以虚线展示预测数据
ts_data_new.plot(label='raw data') # 以实线展示原始数据
plt.legend(loc='best') # 设置图例位置
plt.title('raw data and predicted data with RMSE of %.2f' % RMSE) # 设置标题
plt.show() # 展示图像
return ts # 返回还原后的时间序列
函数功能实现中,通过最优模型的predict方法做时间序列内的数据预测,判断如果数据经过平稳性处理,则将数据做还原处理;由于预测数据比原始时间序列数据的索引少,因此将二者匹配为相同索引下的数据量用于数据比较;通过自定义的公式计算RMSE;最后通过matplotlib分别画出预测数据(虚线表示)、实际数据(实线表示)。
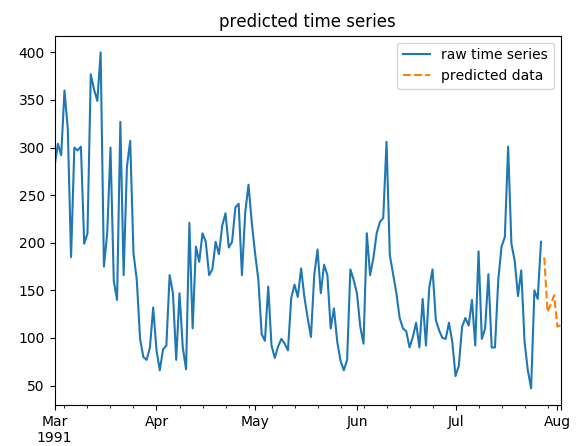
第九部分定义了一个名为predict_data的函数
该函数用来预测未来指定时间项的数据。函数参数:
- model_arma: 最优ARMA模型对象
- ts: 时间序列数据,Series类型
- log_n: 平稳性处理的log的次数,int型
- start: 要预测数据的开始时间索引
- end: 要预测数据的结束时间索引
- rule1: rule1规则布尔值,布尔型
- rule2: rule2规则布尔值,布尔型
返回: 无
# 预测未来指定时间项的数据
def predict_data(model_arma, ts, log_n, start, end, rule1=True, rule2=True):
'''
:param model_arma: 最优ARMA模型对象
:param ts: 时间序列数据,Series类型
:param log_n: 平稳性处理的log的次数,int型
:param start: 要预测数据的开始时间索引
:param end: 要预测数据的结束时间索引
:param rule1: rule1规则布尔值,布尔型
:param rule2: rule2规则布尔值,布尔型
:return: 无
'''
predict_ts = model_arma.predict(start=start, end=end) # 预测未来指定时间项的数据
print ('-----------predict data----------') # 打印标题
if not (rule1 and rule2): # 如果两个条件有任意一个不满足
predict_ts = recover_log(predict_ts, log_n) # 还原数据
print (predict_ts) # 展示预测数据
# 展示预测趋势
plt.figure() # 创建画布
ts.plot(label='raw time series') # 设置推向标签
predict_ts.plot(label='predicted data', style='--') # 以虚线展示预测数据
plt.legend(loc='best') # 设置图例位置
plt.title('predicted time series') # 设置标题
plt.show() # 展示图像
该函数功能的实现中,通过最优模型的predict方法,指定时间序列外的开始和终止时间索引来定义要预测的时间区间;如果预测的结果经过平稳性处理,那么将结果做还原处理;最后通过matplotlib分别将原始时间序列(实现)和预测的时间序列(虚线)输出到一个图像中。
第十部分为整个程序的应用部分 。
分为以下几个步骤:
步骤1 读取数据
先通过lambda函数定义了一个用于将日期解析出来的功能项,功能项的核心是使用lambda表达式配合pandas.datetime中的strptime方法将字符串解析为日期格式,该功能项会在pandas读取数据文件时使用,日期的格式按照源文件的格式来标记,这样能准确解析源文件日期。
# 读取数据
date_parse = lambda dates: pd.datetime.strptime(dates, '%m-%d-%Y') # 创建解析列的功能对象
df = pd.read_table('time_series.txt', delimiter='\t', index_col='date', date_parser=date_parse)
ts_data = df['number'].astype('float32') # 将列转换为float32类型
print ('data summary') # 打印标题
print (ts_data.describe()) # 打印输出时间序列数据概况
在使用pandas的read_table读取数据文件时,通过index_col指定date列为索引列,代替默认的数值索引;通过date_parser参数指定刚才定义的日期解析功能项,由于date_parser默认的日期解析格式为YYYY-MM-DD HH:MM:SS,跟源数据格式不符,因此需要人工自定义格式。
最后应用astype方法将时间序列项的格式类型转换为float32,并通过describe方法输出时间序列概况,结果如下:
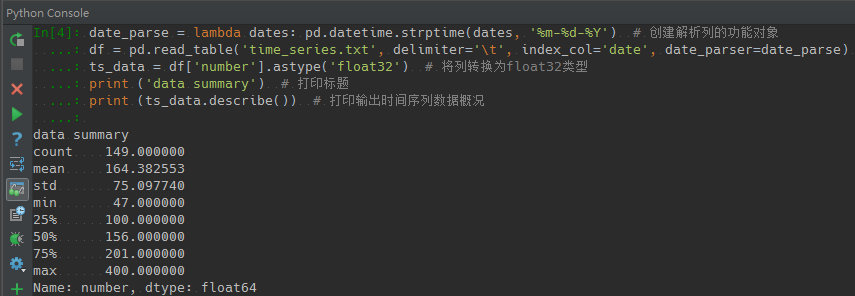
describe方法输出的数据包括数据记录数、均值、标准差、最小值、最大值、25%、50%和75%分位数。
步骤2 原始数据检验
这里直接调用已经定义好的稳定性检验和白噪声检验函数,并传入原始时间序列数据。
# 原始数据检验
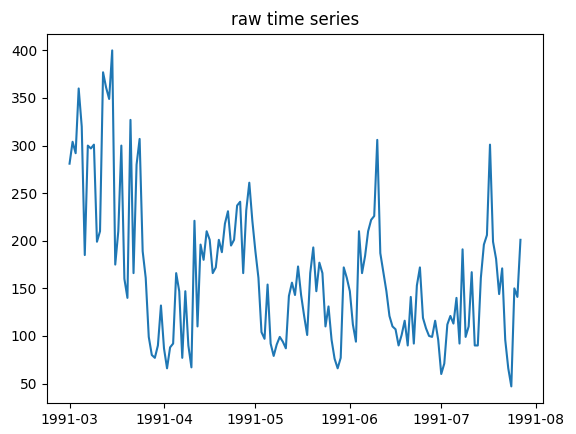
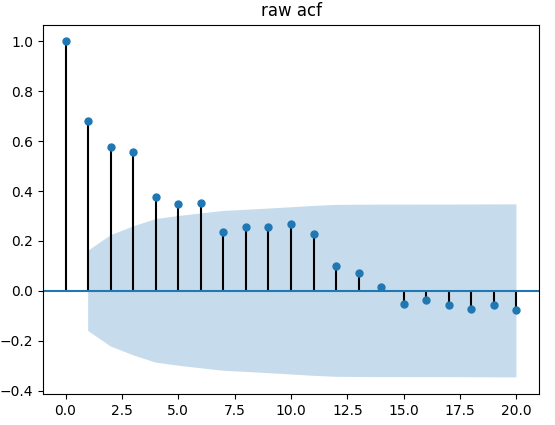
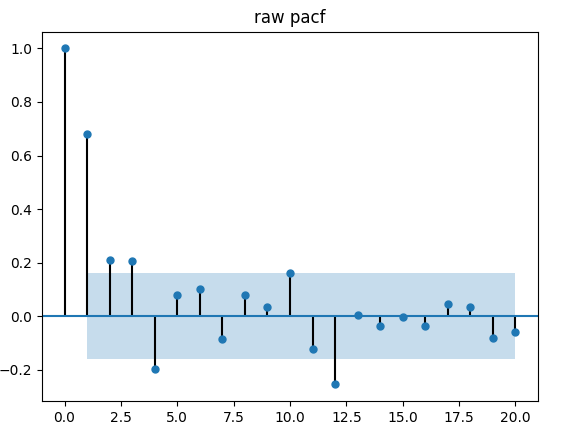
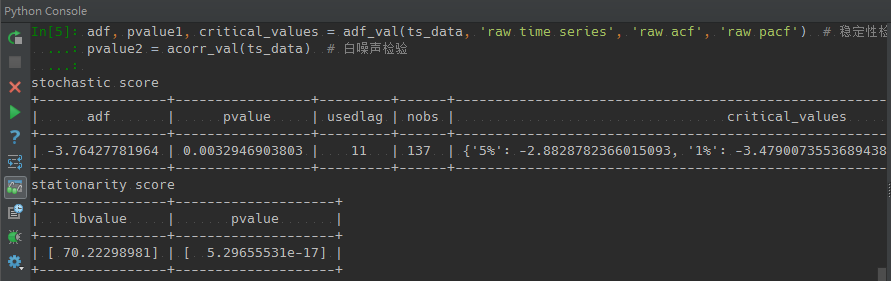
adf, pvalue1, critical_values = adf_val(ts_data, 'raw time series', 'raw acf', 'raw pacf') # 稳定性检验
pvalue2 = acorr_val(ts_data) # 白噪声检验
由原始时间序列图发现,在4月份之前的数据波动较为明显,但4月份之后的数据基本处于平稳波动的状态。
在ACF图中通过配置参数lags=20(20个滞后点)来更清晰的展示数据的分布,前20个滞后点基本已经看出明显趋势。
ADF稳定性检验结果:stochastic score和白噪声检验结果:stationarity score
如何通过上述指标分析数据是稳定且随机分布?如果是时间序列具有稳定性,那么ADF的值(adf)需要小于critical_values中的1%、5%和10%的三个值,且P值(pvalue)一般小于0.01。在白噪声检验结果中,P值需要小于0.05即说明数据是随机分布的。从数据结果看,示例数据恰好能满足条件的定义。
输出的ACF和PACF图更多的用于辅助判断p和q的阶数,通过分析截尾和拖尾的状态来人工判断p和q的值。这里不使用这种方法。
步骤3 创建用于区分是否进行平稳性处理的规则。
该规则使用调用步骤2中返回的结果,在条件的定义中,比较关键的是ADF的P值和白噪声检验的P值的阀值定义,这两个值的定义标准在步骤2的返回结果中已经给出。
# 创建用于区分是否进行平稳性处理的规则
rule1 = (adf < critical_values['1%'] and adf < critical_values['5%'] and adf < critical_values['10%'] and pvalue1 < 0.01) # 稳定性检验
rule2 = (pvalue2[0,] < 0.05) # 白噪声检验
步骤4对时间序列做稳定性处理。
在该步骤中,如果数据符合平稳性,那么不需要做平稳性处理;否则需要处理直到同时满足2个条件的阀值要求。由于示例数据满足稳定性和白噪声检验,因此直接返回0和原始数据集。
# 对时间序列做稳定性处理
log_n, ts_data = get_best_log(ts_data, max_log=5, rule1=rule1, rule2=rule2)
步骤5 再次做检验,包括平稳性和白噪声检验。由于没有做任何处理,返回的结果仍然跟步骤2相同。
adf, pvalue1, critical_values = adf_val(ts_data, 'final time series', 'final acf', 'final pacf') # 稳定性检验
pvalue2 = acorr_val(ts_data) # 白噪声检验
步骤6 训练最佳ARMA模型并输出相关参数和对象。在该步骤中,命令中交互窗口会有警告信息,忽略该信息即可。
# 训练最佳ARMA模型并输出相关参数和对象
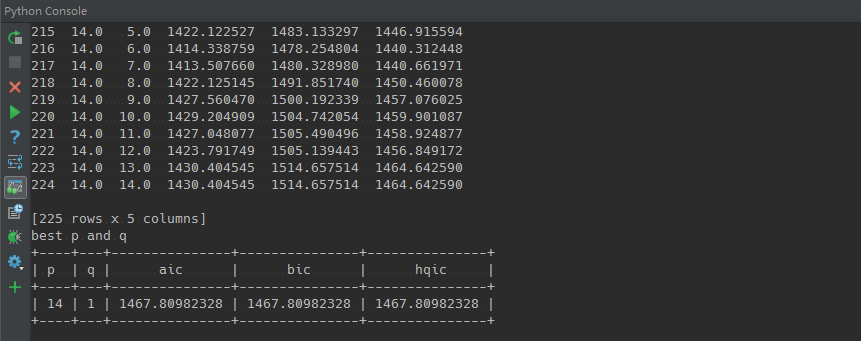
model_arma = arma_fit(ts_data)
该数据是每次训练时取不同p和q计算对应的AIC、BIC和HQIC的值,可通过该数据分析不同训练的结果。
ARMA最优模型下的p和q的值,满足BIC最小的原则。
步骤7模型训练和效果评估。
通过最优的ARMA模型对训练集做时间序列内的预测,并与原始时间序列数据做对比,输入预测值与实际值的时间序列对比趋势图以及RMSE输出预测结果。
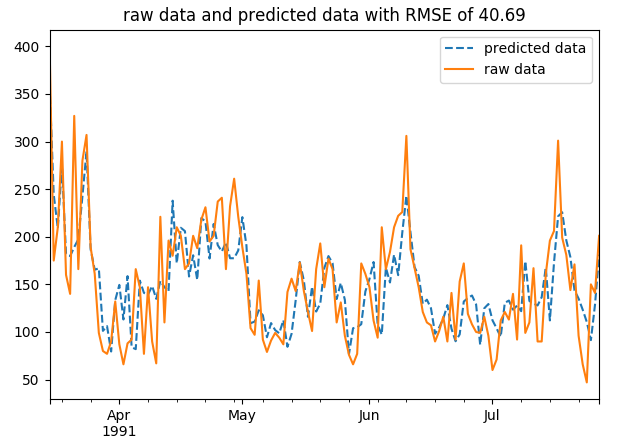
ts_data = train_test(model_arma, ts_data, log_n, rule1=rule1, rule2=rule2)
从对比图中发现,预测值与实际值的数据对比差异不大,并且趋势分布能比较好的还原实际数据分布规律。
步骤8模型预测应用。
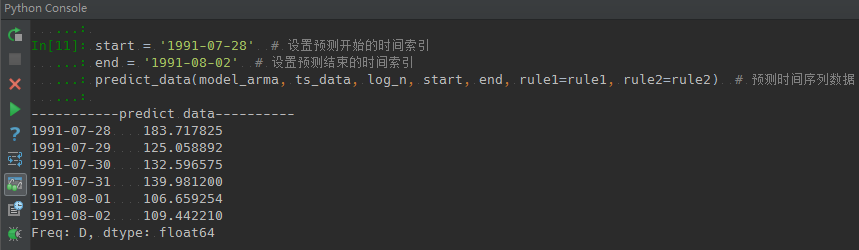
这里设置了预测起止时间分别是1991-07-28、1991-08-02,调用predict_data做预测分析。
start = '1991-07-28' # 设置预测开始的时间索引
end = '1991-08-02' # 设置预测结束的时间索引
predict_data(model_arma, ts_data, log_n, start, end, rule1=rule1, rule2=rule2) # 预测时间序列数据
预测结果与实际结果合成
上述过程中,主要需要考虑的关键点是:
- 如何做数据平稳性处理
- 如何通过ACF和PACF图做p和q阶数评估(当然采用AIC、BIC是一种自动化的方法)
- 在做数据平稳性处理之后,注意还原数据,否则预测数据将难以应用
- ARMA模型在做最优模型训练后,可直接返回模型对象给其他程序调用,而无需重复训练
代码实操小结 :
在本示例的代码中,主要使用了statsmodels的相关库和方法做时间序列的分析处理和预测应用,知识点如下:
- 通过def函数式的方法定义不同的功能模块实现不同的功能,函数中包含参数、功能和返回信息
- 为函数写Doc String
- 使用prettytable库中的add_row、field_names等方法创建格式化表格并输出
- 通过for循环结合多条件语句做循环处理
- 使用numpy的log、exp、sum等方法做基本数据处理
- 使用statsmodels库里面的plot_acf、plot_pacf做acf和pacf图形检验分析,adfuller、acorr_ljungbox做adf检验和随机性检验
- 使用matplolib做折线图输出,并设置不同的线条样式
- 使用ACI、BIC等方法做最优ARMA模型p和q阶数的选择
- 使用自定义方法计算RMSE
- 使用ARMA的fit方法做模型训练,predict方法做时间序列预测
- 使用lambda表达式实现基本功能处理
- 使用datetime中的strptime将字符串转换为日期格式
- 通过pandas的read_csv方法读取数据文件并指定分隔符、索引列和日期解析功能对象
- 使用pandas中的describe方法输出数据框的基本概述信息
有关数据分析与挖掘的更多内容,请查看《Python数据分析与数据化运营》。
建立的arma模型,可以通过statsmodels自带的save函数进行持久化,但会被存储为pickle格式,不便于java读取,向咨询一下,我考虑将训练后的模型应用于java,可有什么好的建议?谢谢!
这个ARIMA里面的取值是根据对数处理的循环次数定的。我尝试使用差分进行平稳处理,然而数据无法还原,不知阁下是否可以指导一二。对数处理总是会出现负值,差分总是会出现NaN,对于没有原始序列的预测值,实在是无力回天。
差分的环境,可以参考下:
对数处理得到负数,是有可能的,例如LOG(0.5) = -0.301029996。具体参考下百度的这个函数图:
https://baike.baidu.com/pic/%E5%AF%B9%E6%95%B0%E5%87%BD%E6%95%B0/6013318/0/b8014a90f603738d0e94646db11bb051f919eca7?fr=lemma&ct=single#aid=0&pic=b8014a90f603738d0e94646db11bb051f919eca7
差分一定会有NaN的,因为要做偏移,最开始或最末尾的值,没有可偏移的计算对象