判别分析(DiscriminantAnalysis)是一种分类方法,它通过一个已知类别的“训练样本”来建立判别准则,并通过预测变量来为未知类别的数据进行分类。线性判别式分析(Linear Discriminant Analysis,简称为LDA)是其中一种,也是模式识别的经典算法,在1996年由Belhumeur引入模式识别和人工智能领域。LDA以Bayes判别思想为基础,当分类只有两种且总体服从多元正态分布条件下,Bayes判别与Fisher判别、距离判别是等价的。
基本思想是将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空间维数的效果,投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离,即模式在该空间中有最佳的可分离性。
在文章《[主成分分析Principal componentanalysis(PCA)]》中曾介绍过数据降维的主成分分析(PCA),LDA与PCA都是常用的降维方法,二者的区别在于:
- 出发思想不同。PCA主要是从特征的协方差角度,去找到比较好的投影方式,即选择样本点投影具有最大方差的方向;而LDA则更多的是考虑了分类标签信息,寻求投影后不同类别之间数据点距离更大化以及同一类别数据点距离最小化,即选择分类性能最好的方向。
- 学习模式不同。PCA属于无监督式学习,因此大多场景下只作为数据处理过程的一部分,需要与其他算法结合使用,例如将PCA与聚类、判别分析、回归分析等组合使用;LDA是一种监督式学习方法,本身除了可以降维外,还可以进行预测应用,因此既可以组合其他模型一起使用,也可以独立使用。
- 降维后可用维度数量不同。LDA降维后最多可生成C-1维子空间(分类标签数-1),因此LDA与原始维度数量无关,只有数据标签分类数量有关;而PCA最多有n维度可用,即最大可以选择全部可用维度。
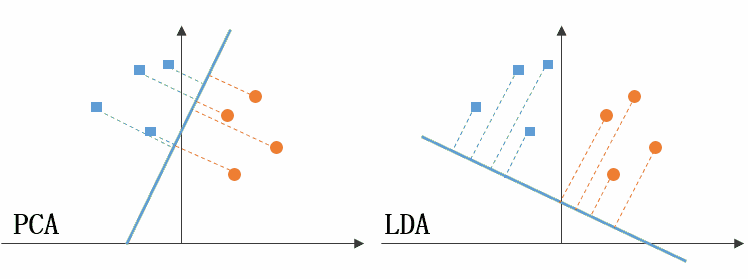
从直接可视化的角度,以二维数据降维为例,PCA和LDA的区别如下图:
上图左侧是PCA的降维思想,它所作的只是将整组数据整体映射到最方便表示这组数据的坐标轴上,映射时没有利用任何数据内部的分类信息。因此,虽然PCA后的数据在表示上更加方便(降低了维数并能最大限度的保持原有信息),但在分类上也许会变得更加困难;上图右侧是LDA的降维思想,可以看到LDA充分利用了数据的分类信息,将两组数据映射到了另外一个坐标轴上,使得数据更易区分了(在低维上就可以区分,减少了运算量)。
线性判别分析LDA算法由于其简单有效性在多个领域都得到了广泛地应用,是目前机器学习、数据挖掘领域经典且热门的一个算法;但是算法本身仍然存在一些局限性:
- 当样本数量远小于样本的特征维数,样本与样本之间的距离变大使得距离度量失效,使LDA算法中的类内、类间离散度矩阵奇异,不能得到最优的投影方向,在人脸识别领域中表现得尤为突出
- LDA不适合对非高斯分布的样本进行降维
- LDA在样本分类信息依赖方差而不是均值时,效果不好
- LDA可能过度拟合数据
以下使用Python的机器学习库SKlearn中的LDA(使用贝叶斯判别)进行案例演示。原始数据集中有4个维度,3个目标分类集。使用其中的最后5个数据作为预测使用,其余作为训练数据。
from sklearn import datasets
from sklearn.lda import LDA
iris = datasets.load_iris()
X = iris.data[:-5]
pre_x = iris.data[-5:]
y = iris.target[:-5]
print ('first 10 raw samples:', X[:10])
clf = LDA()
clf.fit(X, y)
X_r = clf.transform(X)
pre_y = clf.predict(pre_x)
#降维结果
print ('first 10 transformed samples:', X_r[:10])
#预测目标分类结果
print ('predict value:', pre_y)
以下是输出结果,结果看出,原始数据集由于是3个目标分类,因此降维后最多只能产生2个“新维度”: `
('first 10 raw samples:', array([[ 5.1, 3.5, 1.4, 0.2],
[ 4.9, 3. , 1.4, 0.2],
[ 4.7, 3.2, 1.3, 0.2],
[ 4.6, 3.1, 1.5, 0.2],
[ 5. , 3.6, 1.4, 0.2],
[ 5.4, 3.9, 1.7, 0.4],
[ 4.6, 3.4, 1.4, 0.3],
[ 5. , 3.4, 1.5, 0.2],
[ 4.4, 2.9, 1.4, 0.2],
[ 4.9, 3.1, 1.5, 0.1]]))
('first 10 transformed samples:', array([[ 7.82980001, 0.32152479],
[ 6.90948663, -0.79927295],
[ 7.27243493, -0.26853178],
[ 6.60094723, -0.65305491],
[ 7.90146095, 0.54669608],
[ 7.46909339, 1.49939454],
[ 7.00117745, 0.36240908],
[ 7.37793873, 0.01740025],
[ 6.35610395, -1.02010821],
[ 7.11704798, -0.91694247]]))
('predict value:', array([2, 2, 2, 2, 2]))
LDA可配置的参数包括:
class sklearn.lda.LDA(solver='svd', shrinkage=None, priors=None, n_components=None, store_covariance=False, tol=0.0001)
LDA的应用应用场景:
- 人脸识别中的降维或模式识别
- 根据市场宏观经济特征进行经济预测
- 根据市场或用户不同属性进行市场调研
- 根据患者病例特征进行医学病情预测
尾巴
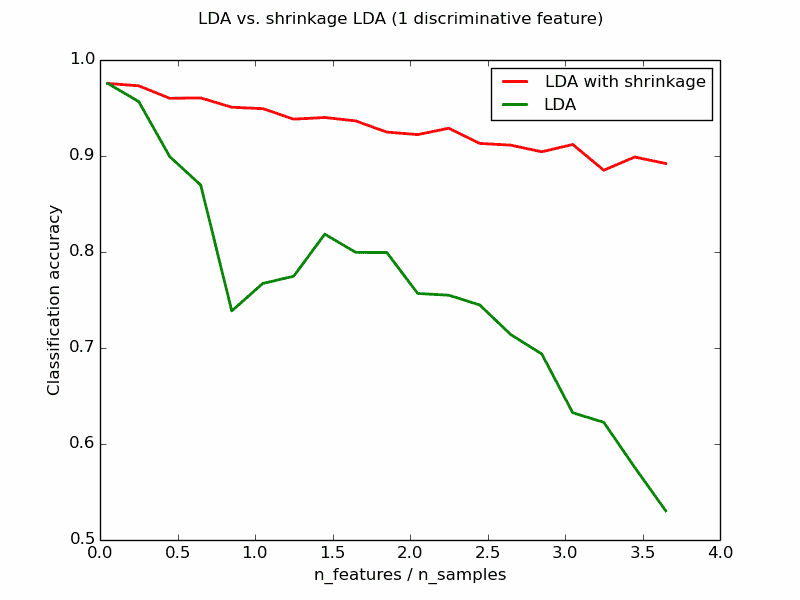
LDA是是一个经典的机器学习算法,它是判别分析中的线性分类器,在很多应用情况下会面临数据稀疏的问题,尤其是在面部识别的场景:数据的维度很可能大于数据的样本量,甚至可能呈几倍的差异。此时,LDA的预测准确率会表现较差,当维度数/样本量达到4倍时,准确率会只有50%左右,解决方法之一是可以对LDA算法进行收缩,Python的SKlearn中的LDA算法支持这一收缩规则。默认情况下,solver的值被设定为“svd”,这在大数据量下的表现很好,但不支持收缩规则;当面临数据稀疏时,我们需要使用“lsqr”或“eigen”,另外,与之配合的是shrinkage参数需要设置成auto以便于算法自动调整收缩值,当然你也可以自己凭借经验将值设定在0~1之间(越大收缩越厉害:0时不收缩,1时意味着对角线方差矩阵将被用作协方差矩阵值的估计)。
对了,最近我也在学习使用scikit_learn,就LDA这个算法。Fisher判别式会学习到一个转换矩阵w对所有特征向量降维操作,我想问一下,sk的LDA算法能否提取出这个w?
博主,最近在看LDA,发现好像有两种版本的解释,一是从贝叶斯角度,二是从Fisher判别角度(最大类间距离和最小类内方差),两者的推导结果不大相同。常见的LDA用于降维,一般是从说法二进行说明。我想问一下,到底两者有何关联?谢谢。
写得很好,受教了。把以前不熟悉的算法补上了。
如果使用LDA做降维的话是怎么使用呢? 降维后的维度大小是否能够受控(像PCA一样由自己制定特征值归零的个数)?或者只能降维到1,还是说根本无法固定呢?