传统的降维方法,包括PCA、LDA等都是以观测数据点呈高斯分布模型为基本假设前提的,在已经先验经验知道观测数据集为非高斯分布模型的前提下,PCA和LDA的降维效果并不好;而本文介绍的ICA将适用于非高斯分析数据集,它是CIA,是主成分分析(PCA)和因子分析(Factor Analysis)的一种有效扩展。 独立成分分析(Independent component analysis,简称ICA)是一种利用统计原理进行计算的方法,它是一个线性变换,这个变换把数据或信号分离成统计独立的非高斯的信号源的线性组合。
独立成分分析的最重要的假设就是信号源统计独立,并且这个假设在大多数盲信号分离(blind signal separation)的情况中符合实际情况;但即使当该假设不满足时,仍然可以用独立成分分析来把观察信号统计独立化,从而进一步分析数据的特性。
独立成分分析并不能完全恢复信号源的具体数值,也不能解出信号源的正负符号、信号的级数或者信号的数值范围,它能做的是将不同独立的信号源进行按照特征进行分离。
ICA应用前提很简单:数据信号源是独立的且数据非高斯分布(或者信号源中最多只有一个成分是高斯分布),另外观测信号源的数目不能少于源信号数目(为了方便一般要求二者相等即可)。
下面应用Python机器学习库SKlearn中的FastICA来演示信号分离并与PCA进行对比的案例。 `
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from sklearn.decomposition import FastICA, PCA
# 生成观测模拟数据
np.random.seed(0)
n_samples = 2000
time = np.linspace(0, 8, n_samples)
s1 = np.sin(2 * time) # 信号源 1 : 正弦信号
s2 = np.sign(np.sin(3 * time)) # 信号源 2 : 方形信号
s3 = signal.sawtooth(2 * np.pi * time) # 信号源 3: 锯齿波信号
S = np.c_[s1, s2, s3]
S += 0.2 * np.random.normal(size=S.shape) # 增加噪音数据
S /= S.std(axis=0) # 标准化
# 混合数据
A = np.array([[1, 1, 1], [0.5, 2, 1.0], [1.5, 1.0, 2.0]]) # 混合矩阵
X = np.dot(S, A.T) # 生成观测信号源
# ICA模型
ica = FastICA(n_components=3)
S_ = ica.fit_transform(X) # 重构信号
A_ = ica.mixing_ # 获得估计混合后的矩阵
# PCA模型
pca = PCA(n_components=3)
H = pca.fit_transform(X) # 基于PCA的成分正交重构信号源
# 图形展示
plt.figure()
models = [X, S, S_, H]
names = ['Observations (mixed signal)','True Sources','ICA recovered signals','PCA recovered signals']
colors = ['red', 'steelblue', 'orange']
for ii, (model, name) in enumerate(zip(models, names), 1):
plt.subplot(4, 1, ii)
plt.title(name)
for sig, color in zip(model.T, colors):
plt.plot(sig, color=color)
plt.subplots_adjust(0.09, 0.04, 0.94, 0.94, 0.26, 0.46)
plt.show()
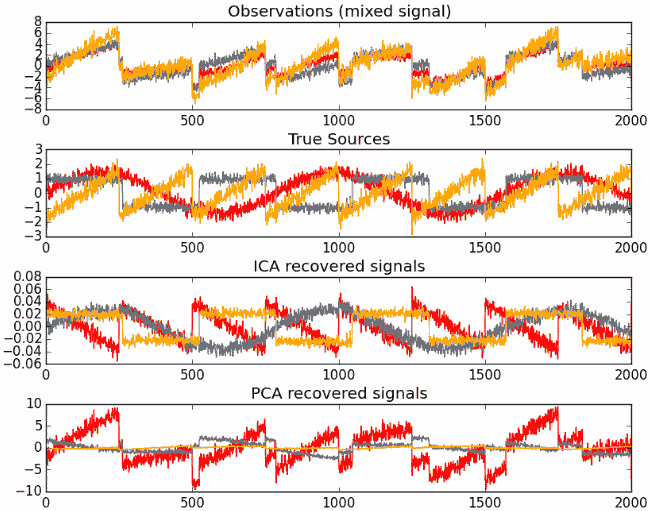
代码运行的结果如下:
由结果可知,原始观测信号源有3种独立信号源混合(正弦、方形和锯齿波形),通过ICA可以较好的分离出三种信号源,而PCA的分离效果不佳,只分离出一个信号源。
ICA的经典问题是“鸡尾酒会问题”(cocktail party problem),这个问题假设在party(或鸡尾酒会)中有n个人,我们利用房间里面的n个麦克风或录音机对同时说话的这些人进行录音,由此得到一个混合信号源或声音源,现在要做的就是从这个信号源中分离出不同人的说话声音。
独立成分分析法(ICA)最初是用来解决“鸡尾酒会”的问题,ICA基于信号高阶统计特性的分析方法,经ICA分解出的各信号成分(或者叫分量)之间是相互独立的,正是因为这一特点,ICA在信号处理领域受到了广泛的关注。除了经典的盲源分离外,它的应用领域还包括:
- 图像识别,去除噪音信息
- 语言识别,分离音源并去除噪音(如去除噪音只保留输入语音)
- 通信、生物医学信号处理,从这些信号中单独区分某些信号(如区分胎儿和孕妇的心电信号)
- 故障诊断,去除非自然信息
- 特征提取和降维
- 自然信息处理,如地震声音分离
FastICA可配置的参数如下: `
class sklearn.decomposition.FastICA(n_components=None, algorithm='parallel', whiten=True, fun='logcosh', fun_args=None, max_iter=200, tol=0.0001, w_init=None, random_state=None)
尾巴
盲源分离中的盲源指的是源信号不可观测且混合特性不可知,很多时候盲源分离(blind signal separation)会被称为独立成分分析,但其实仅当盲源中的不同信号源相互独立时,盲源分离才与独立成分分析等价。因此,独立成分分析是盲源分离的一种特例。因为很多时候,混合信号源是不独立的。